Understanding how to calculate home appreciation is a required skill for any real estate investor. Fortunately, there is a straightforward formula that you can use to work out the future value of your house.
Side note – If you just want to quickly calculate the value of your home, check out our super simple home appreciation calculator.
The goal of this post is to explain how the home appreciation formula works, so you can work out the future market value of an investment property or your personal residence. We have also included a section on how to calculate property appreciation using Excel, and there are plenty of examples to clarify things along the way. In addition, it is worth mentioning that understanding real estate appreciation is the key to calculating how much home equity you have built up since purchasing the house.
Table of Contents - How To Calculate Appreciation
Quick Way To Calculate Home Appreciation
Simply enter the current value of the property, the home appreciation rate, and the number of years into the tool below. It will provide the future value of the home.
What Is The Home Appreciation Formula?
F = P * (1 + i)ⁿ
- F = Future Value of Home
- P = Present Value of Home
- i = Interest Rate
- n = Time in years
As you can see from the formula above, there are 3 variables that you need to know in order to work out the future value of your home, namely:
1. Present Value Of Home
This is the current home value, or the market value of the home. You can also use the home price that you paid for the property initially if you want to work out how much it has appreciated since you purchased it.
2. Interest Rate
This is a realistic estimate of property appreciation rates in your area. 3% is a relatively safe bet if you aren’t sure. This is also called the annual appreciation rate.
With that being said, interest rates do fluctuate and the real estate industry is not immune to periods of depreciation. For instance, the global financial crisis in 2008 caused the property bubble to burst, while US property prices have increased dramatically over the last two years.
3. Number of years
Simply put, you need to enter the time period in order to calculate the future value of a property. It is most typical to do this in years, given that properties tend to work according to annual interest rates.
Example of How To Calculate Home Appreciation
Let’s assume that you purchased a $250,000 house, and you want to know what the property value will be 5 years from now. In this example, we will also assume that the annual appreciation rate will be 4% over this time period. Now we simply need to plug these details into the home appreciation formula.
Property Details
- Present Value of property: $250,000
- Interest Rate: 4%
- Time Period: 5 Years
Home Appreciation Formula
- F = P * (1 + i)ⁿ
- F = $250,000 (1 + 0,04)5
- F = $304,163,23
It is important to point out that the calculators on most Smartphones can easily handle inputs for the future value formula. So you can literally estimate the future value of your home using your phone.
How To Calculate Home Appreciation In Excel
Excel Step 1: Enter The Property Details
- Enter the property value
- Enter the interest rate
- Enter the time period
This should leave you with something like this

Excel Step 2: Add The Following Formula To A New Line
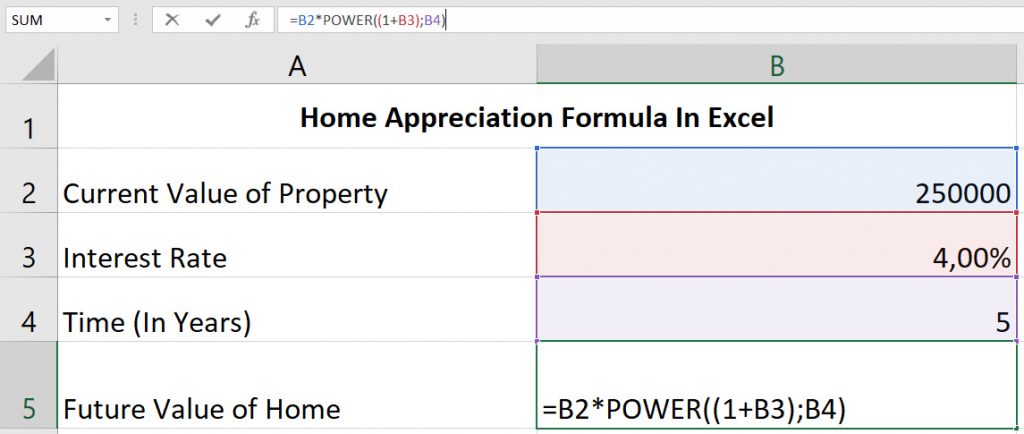
The trick in this example is understanding how to use the POWER function in Excel, given that the home appreciation formula makes use of an exponent.
To make it a bit simpler to understand, take a look at the table below. It shows the standard formula, and what that formula looks like inside Excel (or Google Sheets).
This is the standard formula
F = P * (1 + i)ⁿ
This is what it looks like in Excel
F = P * POWER ((1 + i); n)
- F = Future Value of Home
- P = Present Value of Home
- i = Interest Rate
- n = Time in years
Final Thoughts
In the end, it should be pretty clear that the home appreciation formula offers a reasonably straightforward way to calculate the future value of a real estate investment, regardless of whether it is the home you live in or an investment property. Armed with the initial value of the home, the time period, and the capital appreciation rate, you can easily calculate the final value of the house.
However, if you simply want to do this quickly without understanding all the nuts and bolts, an online home appreciation calculator will suit your needs perfectly.
Frequently Asked Questions (FAQ)
What will my house be worth in 10 years?
To work out the value of your house in 10 years’ time, you need to know three things.
- The current value of your house
- An estimate of the appreciation rate (the expected interest rate for properties in your area)
- Time period – In this case, the time is clearly 10 years.
Armed with these 3 pieces of information, you can work out the expected value of your home in 10 years. You simply need to enter these details into the home appreciation formula (see example further up the article) or use a home appreciation calculator.
Does Home Appreciation Use Simple or Compound Interest?
Provided you are calculating the value of your home over more than one year, home appreciation relies on compound interest. This is mainly because the value of the home changes every year. The compound interest formula factors this change of value into the equation. The simple interest formula does not.
To further demonstrate the difference between simple and compound interest for home appreciation specifically, consider the table below. It outlines the value of a home over 10 years using simple interest compared to the value of a home over 5 years using compound interest.
Simple Interest vs Compound Interest Example
- Property Price: $200,000
- Interest Rate: 6%
- Time Period: 10 Years
| Simple Interest Formula | Compound Interest Formula |
| F = P (1 + i * n) | F = P * (1 + i)ⁿ |
| Year 1: $212,000.00 | Year 1: $212,000.00 |
| Year 2: $224,000.00 | Year 2: $224,720.00 |
| Year 3: $236,000,00 | Year 3: $238,203.20 |
| Year 4: $248,000.00 | Year 4: $252 495,39 |
| Year 5: $260 000,00 | Year 5: $267 645,12 |
| Year 6: $272 000,00 | Year 6: $283 703,82 |
| Year 7: $284 000,00 | Year 7: $300 726,05 |
| Year 8: $296 000,00 | Year 8: $318 769,61 |
| Year 9: $308 000,00 | Year 9: $337 895,79 |
| Year 10: $320 000,00 | Year 10: $358 169,54 |
Ultimately it doesn’t make sense to use the simple interest formula for home appreciation. Doing so ignores the fact that the property has increased in value over the time period (assuming the interest rate is positive).
Conversely, it makes perfect sense to use the compound interest formula for home appreciation. The compound interest formula dynamically updates the value of the home each year, resulting in a much more accurate calculation of the future value of the house.